Николаев Сергей Викторович
Николаев Сергей Викторович
Должность: доцент
Стаж работы:
общий: 23 года
по специальности: 21 год
Контактная информация:
тел.: +7-(391)-206-21-17
e-mail: svinikolaev@sfu-kras.ru
Совместительство: Институт физики им. Л.В. Киренского СО РАН, научный сотрудник лаборатории Физики магнитных явлений, адрес: ул. Академгородок, 50, стр.38, ком.3-066.
Образование:
2021 – Почётная грамота Министерства науки и высшего образования Российской Федерации.
2021 – присвоено учёное звание доцента по специальности «Теоретическая физика».
2006 – к.ф.-м.н., 01.04.07 Физика конденсированного состояния, «Исследование процесса проскальзывания фазы в сверхпроводящей нанопроволоке».
2004 – окончил с отличием Омский государственный университет по специальности «Физика», квалификация «Физик».
Повышение квалификации:
- «Подготовка к прохождению государственной аккредитации образовательной деятельности: фонд оценочных средств» (40 ч., Удостоверение № 93/25-Б1932), СФУ, с 15.04.2025 года по 02.06.2025 года
- «Подготовка к прохождению государственной аккредитации образовательной деятельности: оценочные материалы для диагностической работы по проверке сформированности компетенций» (40 ч., Удостоверение № 93/25-Б1867), СФУ, с 15.04.2025 года по 02.06.2025 года
- «Введение в искусственный интеллект» (36 ч., Удостоверение № 93/23-Б2921), СФУ, с 02.10.2023 года по 08.12.2023 года
- «Проведение экспортного контроля в высшем учебном заведении» (36 ч., Удостоверение № 93/22-Б1380), СФУ, с 03.10.2022 года по 01.11.2022 года
- «Корпоративные сервисы СФУ» (18 ч., Удостоверение № 93/22-Э082), СФУ, с 14.03.2022 года по 25.03.2022 года
- «Английский язык для преподавателей университетов неязыковых специальностей (B2)» (96 ч., Удостоверение № 26-1/18-Б334), СФУ, с 11.09.2017 г. по 05.02.2018 г.
- «Международная летняя суперкомпьютерная академия МГУ» (36 ч., Сертификат № СА 0732), МГУ, с 23.06.2017 года по 01.07.2017 года
- «Подготовка к Кембриджским экзаменам — FCE» (240 ч., Удостоверение № 26-1/17-Б327), СФУ, с 19.09.2016 года по 10.06.2017 года
- «English for Scientists» (144 ч., Удостоверение № 26-1/16-Б351), СФУ, с 15.09.2015 года по 15.05.2016 года
- «Международная летняя суперкомпьютерная академия МГУ» (100 ч., Сертификат № СА 0462), МГУ, с 22.06.2015 года по 03.07.2015 года
- «Разработка электронных ресурсов в системе LMS Moodle» и «Система «Антиплагиат» введение в Mind» (40 ч., Сертификат № 26-1/15-Э417), СФУ, с 24.02.2015 года по 29.05.2015 года
- «Электронные информационные ресурсы для образования» (18 ч., Сертификат № 26-1/15-Э794), СФУ, с 23.11.2015 года по 25.12.2015 года
Преподаваемые дисциплины:
- Вычислительная физика
- Численные методы и математическое моделирование
- Квантовая механика
- Численные методы в статистической физике
- Численные методы в теории сильно коррелированных систем
- Специализированные компьютерные технологии в физике
Учебно-методические разработки:
- Теория колебаний и волн. Практические занятия. Часть 1. Системы с одной степенью свободы : учебно-методическое пособие / Сиб. федер. ун-т, Ин-т инж. физики и радиоэлектроники ; сост.: М. В. Зотова, С. В. Николаев, А. Р. Коловский. — Электрон. текстовые дан. (pdf, 1 Мб). — Красноярск : СФУ, 2023 (2023-02-13). — 30 с. — Загл. с титул. экрана. — Изд. № 2023-18265 : Б. ц. — Текст : электронный.
- Квантовая механика : учебно-методическое пособие / С. В. Николаев, Ю. С. Орлов, А. С. Федоров ; Сиб. федер. ун-т, Ин-т инж. физики и радиоэлектроники. — Красноярск : СФУ, 2020 (2020-06-10). — 128 с.
- Численные методы и математическое моделирование : учебно-методическое пособие / Сиб. федер. ун-т, Ин-т инж. физики и радиоэлектроники ; сост.: С. В. Николаев, Ю. С. Орлов. — Красноярск : СФУ, 2019. — 49 с.
- Электродинамика : учебно-методическое пособие / М-во науки и высш. образования Рос. Федер., Сиб. федер. ун-т, Ин-т инж. физики и радиоэлектроники ; [сост.: Ю. С. Орлов, С. В. Николаев]. — Красноярск : СФУ, 2019. — 159 с.
- Специализированные компьютерные технологии в физике : [учеб-метод. материалы к изучению дисциплины для …03.04.02.05 Теоретическая и математическая физика] / С. В. Николаев. — Красноярск : СФУ, 2018. — Б. ц. — Текст : электронный.
- Численные методы в статистической физике : [учеб-метод. материалы к изучению дисциплины для …03.04.02.05 Теоретическая и математическая физика] / С. В. Николаев. — Красноярск : СФУ, 2018. — Б. ц. — Текст : электронный.
- Квантовая механика : [учеб-метод. материалы к изучению дисциплины для …03.03.02 Физика, 03.03.02.01 Фундаментальная физика, 03.03.02.07 Биохимическая физика, 14.03.02 Ядерные физика и технологии, 16.03.01 Техническая физика, 28.03.01.02 Материалы микро- и наносистемной техники] / А.С. Федоров, С.В. Николаев. — Красноярск : СФУ, 2018. — Б. ц. — Текст : электронный.
- Квантовая механика : учебно-методическое пособие для семинарских занятий и самостоятельной работы [для студентов спец. 010700.62 «Физика»] / Сиб. федерал. ун-т ; сост. А. С. Федоров [и др.]. — Красноярск : СФУ, 2012. — 38 с.
- Численные методы и математическое моделирование : учеб. — метод. пособие для лабораторного практикума и самостоятельной работы [для студ. напр. 010700.62 «Физика»] / Сиб. федерал. ун-т ; сост. С. В. Николаев. — Красноярск : СФУ, 2012. — 46 с.
Руководство (соруководство) аспирантами, магистрантами, бакалаврами:
- руководство аспирантом (СФУ) – Кальдин Р.А.
Научные интересы:
- Сильно коррелированные электронные системы
- Теория высокотемпературной сверхпроводимости
- Электронные и магнитные свойства материалов
- Численные методы
- Нелинейные явления в наносистемах
- Ультрахолодные атомы в оптических ловушках
Аннотация научных исследований:
Мои научные исследования связаны с решением фундаментальных проблем высокотемпературной сверхпроводимости (ВТСП). Основная цель исследований заключается в том, чтобы лучше понять природу ВТСП и получить новые данные об особенностях электронной структуры и свойствах нормального и сверхпроводящего состояний. Важным этапом исследования ВТСП материалов является учёт сильных электронных корреляций (СЭК), которые играют существенную роль в формировании электронных свойств нормальной и сверхпроводящей фаз. Известно, что учёт СЭК наиболее адекватно происходит в рамках кластерных подходов [T. Maier, M. Jarrell, T. Pruschke, and M.H. Hettler, Rev. Mod. Phys. 77, 1027 (2005)], которые в последнее время получили широкое распространение. Несколько лет назад в теоргруппе профессора Овчинникова С.Г. мы начали разрабатывать новый кластерный подход — кластерную теорию возмущений в представлении Х-операторов Хаббарда.
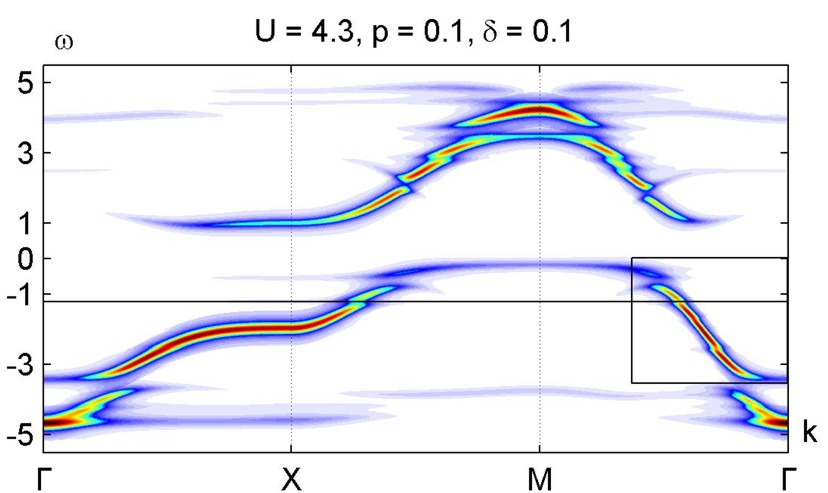
Рисунок 1. Дисперсия вдоль симметричного направления в первой четверти первой зоны Бриллюэна.
Сама идея разбить всю решётку на кластеры и учитывать взаимодействия внутри кластера точно, а взаимодействие между кластерами учесть по теории возмущений, возникла достаточно давно [А.Ф. Барабанов, Л.А. Максимов, А.В. Михеенков, ФТТ 30, 2518 (1988); S.G. Ovchinnikov and I.S. Sandalov, Physica C 161, 607 (1989)]. В последующем были разработаны несколько теорий, основанных на этом принципе, например, кластерная теория динамического среднего поля (в англоязычном сокращении, CDMFT) [G. Kotliar, S.Y. Savrasov, G. Pallson, and G. Biroli, Phys. Rev. Lett. 87, 186401 (2001)], приближение динамического кластера (DCA) [M.H. Hettler, A.N. Tahvildar-Zadeh, M. Jarrell et al, Phys. Rev. B 58, R7475 (1998)], кластерная теория возмущений (CPT) [D. Senechal, D. Perez, and M. Pioro-Ladriere, Phys. Rev. Lett. 84, 522 (2000)].
Первым этапом кластерной теории является разбиение всей решётки на кластеры и точный учёт внутрикластерных взаимодействий. В нашем подходе [С.В. Николаев, С.Г. Овчинников, ЖЭТФ 138, 717 (2010)] мы используем метод полной точной диагонализации с учётом всех возбужденных состояний в каждом подпространстве гильбертова пространства локальных состояний кластера. Используя полный точный набор состояний кластера, можно построить соответствующие кластерные Х операторы Хаббарда. Далее гамильтониан системы переписывается на языке этих операторов (Х-представление). Данное представление позволяет достаточно просто перейти от гамильтониана первоначальной решётки к кластерному гамильтониану и получить решение для функции Грина в приближении «Хаббард-I». Причем Х-представление позволяет ввести понятие f фактора, который определяет меру спектрального веса фермиевской квазичастицы. Контроль этой величины на первых этапах расчёта позволяет существенно сократить машинное время вычислений, не внося существенных искажений в конечный результат расчёта. Вторым этапом построения кластерной теории является учёт межкластерных взаимодействий. В разработанном подходе мы используем технику X-операторов Хаббарда, которая позволяет непосредственно и точно записать взаимодействие между кластерами на языке Х-операторов.
В рамках развиваемой нами кластерной теории возмущений рассчитывается одноэлектронная функция Грина и соответствующая спектральная функция, которая позволяет получить карты распределения спектрального веса квазичастиц в первой зоне Бриллюэна, плотность состояний и закон дисперсии с учётом спектрального веса (см. рисунок 1). По распределению спектрального веса в первой зоне Бриллюэна можно восстановить поверхность Ферми и провести сравнение с экспериментальными данными по фотоэмиссионной спектроскопии с угловым разрешением (ARPES).
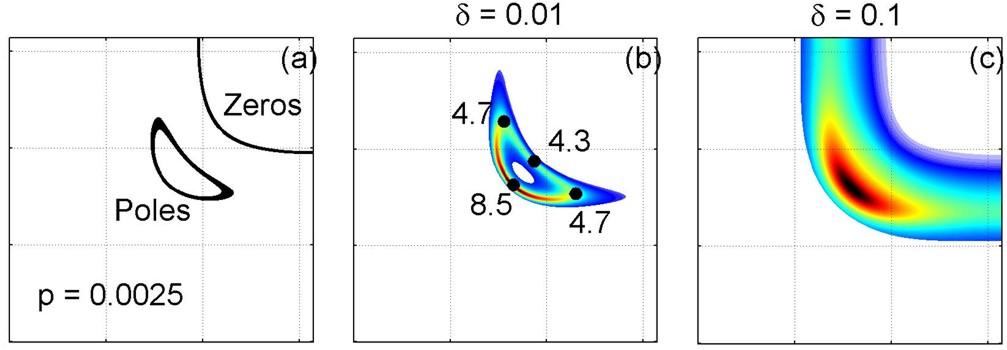
Рисунок 2. Полюса и нули функции Грина (a) и соответствующие карты распределения спектрального веса в первой четверти первой зоны Бриллюэна при параметре уширения спектральных линий 0.01 (b) и 0.1 (c).
Применение разработанного подхода к исследованию двумерной решётки в рамках однозонной модели Хаббарда позволило выявить неоднородное распределение спектрального веса вдоль поверхности Ферми (арочная структура) (см. рисунок 2), которое хорошо согласуется с экспериментами ARPES. Исследование от величины дырочного допирования позволило выявить каскад квантовых фазовых переходов и дырочный карман в нодальном направлении в области слабого допирования [С.В. Николаев, С.Г. Овчинников, ЖЭТФ 141, 135 (2012)]. Также в рамках данного подхода проведены исследования электронных свойств нормальной фазы для t-J и t-J* моделей, которые являются наиболее адекватными моделями для ВТСП купратов [V.I. Kuz’min, S.V. Nikolaev and S.G. Ovchinnikov, Physical Review B 90, 245104 (2014)]. Причём в рамках данных моделей мы провели исследование трансформации электронной структуры от величины внешнего магнитного поля и показали, что поверхности Ферми, получаемые методами ARPES без магнитного поля, и поверхности Ферми в сильных полях по данным квантовых осцилляций, вообще говоря, могут относиться к разным электронным структурам, разделенным друг от друга обнаруженным нами скачкообразным изменением в магнитном поле.
В настоящее время в рамках кластерного подхода мы проводим исследование многозонной модели Хаббарда, которая является хорошим приближением для описания физических свойств нового класса ВТСП соединений, открытых в 2008 году, — пниктидов. Также сейчас мы проводим исследование ультрахолодных бозе-атомов в оптических ловушках в рамках кластерного обобщения модели Бозе-Хаббарда. В этом случае кластерный подход является наиболее приемлемым, так как пространственное разделение решётки на кластеры можно организовать в настоящих экспериментах и, таким образом, провести количественное сравнение результатов численного расчёта с экспериментальными данными.
Перечень публикаций (по данным scholar.sfu-kras.ru):
| Базы данных: | |||||
|---|---|---|---|---|---|
| Количество публикаций: | 72 | 30 | 27 | ||
| Всего публикаций: 76 | |||||
- РАЗРАБОТКА ЛИЧНОГО КАБИНЕТА ТОРГОВОГО ПРЕДСТАВИТЕЛЯ В ЦИФРОВОЙ ЭКОСИСТЕМЕ ПРЕДПРИЯТИЯ : научное издание [статья из журнала]2025, Научно-технический вестник Поволжья
- Interrelation between Doping Dependencies of the Spin Susceptibility and Electronic Structure in Cuprates : научное издание [статья из журнала]2024, JETP Letters
- Взаимосвязь концентрационных зависимостей спиновой восприимчивости и электронной структуры в купратах : научное издание [статья из журнала]2024, Письма в Журнал экспериментальной и теоретической физики
- Фотоиндуцированная нелинейная динамика сильно коррелированных систем со спиновым кроссовером: автокаталитический спиновый переход : научное издание [статья из журнала]2024, Письма в Журнал экспериментальной и теоретической физики
- Photoinduced Nonlinear Dynamics of Strongly Correlated Systems with Spin Crossover: Autocatalytic Spin Transition : научное издание [статья из журнала]2024, JETP Letters
- Photoinduced Enhancement of the Excitonic Order in Strongly Correlated Electron Systems with the Spin Crossover : научное издание [статья из журнала]2023, JETP Letters
- Excitonic Order in Strongly Correlated Systems with the Spin Crossover : научное издание [статья из журнала]2023, JETP Letters
- Magnetic transitions and excitonic order enhancement in spin crossover strongly correlated electron systems : научное издание [статья из журнала]2023, Materials Today Communications
- РАЗРАБОТКА ИНФОРМАЦИОННОЙ СИСТЕМЫ ДЛЯ СОВМЕСТНОГО ПРОГНОЗИРОВАНИЯ ПРОДАЖ С ПРОИЗВОДИТЕЛЕМ : доклад, тезисы доклада [доклад, тезисы доклада, статья из сборника материалов конференций]2023, Решетневские чтения
- РАЗРАБОТКА СППР ДЛЯ ТОРГОВОГО ПРЕДПРИЯТИЯ : доклад, тезисы доклада [доклад, тезисы доклада, статья из сборника материалов конференций]2023, Актуальные проблемы авиации и космонавтики
Избранные публикации:
- Yu.S. Orlov, S.V. Nikolaev, V.A. Gavrichkov, S.G. Ovchinnikov, Exchange interaction between the high spin Co3+ states in LaCoO3 // Computational Materials Science. — 2022. — Vol. 204. — Pp. 111134.
- E.I. Shneyder, M.V. Zotova, S.V. Nikolaev, S.G. Ovchinnikov, Phonon-assisted insulator-metal transitions in correlated systems driven by doping // Phys.Rev.B. – 2021. – Vol. 104. – Pp. 155153(6).
- Yu.S. Orlov, S.V. Nikolaev, V.A. Dudnikov, S.G. Ovchinnikov, Forming a dielectric exciton phase in strongly correlated systems with spin crossover // Phys.Rev.B. — 2021. — Vol. 104. — Pp. 195103(10).
- Ю.С. Орлов, С.В. Николаев, В.А. Дудников, Влияние кристаллического поля на электронную структуру двухзонной модели Хаббарда со спиновым кроссовером // Журнал экспериментальной и теоретической физики. – 2020. – Т. 157, № 5. – С. 834–846.
- V.I. Kuz’min, M.A. Visotin, S.V. Nikolaev, S.G. Ovchinnikov, Doping and temperature evolution of pseudogap and spin-spin correlations in the two-dimensional Hubbard model // Phys.Rev.B. — 2020. — Vol. 101. — Pp. 115141 (12).
- E.I. Shneyder, S.V. Nikolaev, M.V. Zotova, R.A. Kaldin, S.G. Ovchinnikov, Polaron transformations in the realistic model of the strongly correlated electron system // Phys.Rev.B. — 2020. — Vol. 101. — Pp. 235114 (14).
- Nesterov I., Orlov Yu.S., Ovchinnikov S.G., Nikolaev S.V. Cooperative phenomena in spin crossover systems // Phys.Rev.B. — 2017. — Vol. 96. — Pp. 134103. DOI: 10.1103/PhysRevB.96.13410
- K. Kudashkin, S. Nikolaev, S. Ovchinnikov, Spectral Properties of the Bose-Hubbard Model Within the Cluster Perturbation Theory in X-Operators Representation // Journal of Superconductivity and Novel Magnetism. – 2017. — V. 30, No 1. — Pp. 103-107. DOI: 10.1007/s10948-016-3781-y
- S.V. Nikolaev, M.M. Korshunov, Spin and Charge Susceptibilities of the Two-Orbital Model within the Cluster Perturbation Theory for Fe-Based Materials // Journal of Superconductivity and Novel Magnetism. – 2016. — V. 29, No 12. — Pp. 3093-3097.
- В.И. Кузьмин, С.В. Николаев, С.Г. Овчинников, Влияние скошенного антиферромагнитного порядка на электронную структуру в t-J*-модели в рамках кластерной теории возмущений // Журнал экспериментальной и теоретической физики. – 2016. – Т. 150, № 3(9). – С. 592-601.
- V.I. Kuz’min, S.V. Nikolaev and S.G. Ovchinnikov, Influence of varying magnetic order in external magnetic field on the electronic structure and Fermi surface within the t−J model // Pis’ma v ZhETF. — 2016. — V. 103, iss. 2. — Pp. 132-137
- V.I. Kuz’min, S.V. Nikolaev and S.G. Ovchinnikov, Comparison of the electronic structure of the Hubbard and t-J models within the cluster perturbation theory // Physical Review B 90, 245104 (2014)
- A. Krinitsyn, S. Nikolaev, S. Ovchinnikov, Cluster Size and Shape Effect on the Electronic Structure of the Hubbard ModelWithin the Norm-Conserving Cluster Perturbation Theory // J. Supercond. Nov. Magn. 27, 955 (2014).
- С.В. Николаев, С.Г. Овчинников, Влияние дырочного допирования на электронную структуру и поверхность Ферми в модели Хаббарда в рамках кластерной теории возмущений с контролируемым спектральным весом // Журнал экспериментальной и теоретической физики. 2012. Т.141. № 1. С.135-150.
- S.G. Ovchinnikov, S.V. Nikolaev, The calculation of the Fermi surface with complex topology from norm-conserving cluster perturbation theory for doping dependent electronic structure of the Hubbard model // Pis’ma v ZhETF, 2011. Vol. 93, iss. 9, pp. 575-578.
- Николаев С.В., Овчинников С.Г. Кластерная теория возмущений для модели Хаббарда с точным учетом ближнего магнитного порядка в кластере 2×2 // ЖЭТФ. 2010. Т.138. № 4. С.717-728.
- Николаев С.В., Югай К.Н. Динамические свойства сверхпроводящей нанопроволоки // Журнал экспериментальной и теоретической физики. 2006. Т.129. № 2. С.371-377.
- Nikolaev S.V., Yugay K.N., Kim J.U., and Huh Y. Dynamical Phase Slipping in Superconducting Nanowires // Journal of superconductivity: incorporating novel magnetism. 2005. V.18. No.2. P.261-268.
Гранты:
- «Нелинейная динамика и фотоиндуцированные динамические фазовые переходы в сильно коррелированных системах со спиновым кроссовером», РНФ № 22-22-20007, 2022-2023 гг.
- «Исследования суперобменного и электрон-фононного взаимодействий в коррелированных системах как основа поиска перспективных функциональных материалов», РФФИ № 20-42-240016 р_а, 2020-2021 гг.
- «Эффекты электронных корреляций и многоорбитальная физика в соединениях железа и купратах», РФФИ № 19-42-240007 р_а, 2019-2020 гг.
- «Влияние обменного взаимодействия между возбужденными термами на магнитные свойства и спиновые кроссоверы в равновесных и неравновесных условиях», РНФ № 18-12-00022, 2018-2020 гг.
- «Исследование спектральных свойств сильно коррелированных ультрахолодных атомов в двумерных оптических решётках», РФФИ-ККФН № 16-42-243048, 2016-2017 гг.
- «Влияние кооперативных эффектов на физические свойства магнитных диэлектриков со спиновыми кроссоверами», РФФИ-ККФН № 16-42-240413, 2016-2017 гг.
- «Корреляции и беспорядок в сверхпроводниках на основе железа и купратах», РФФИ № 16-02-00098, 2016-2018 гг.
- «Теоретические и экспериментальные исследования низкомерных систем с сильными электронными корреляциями», Грант президента РФ — ведущая научная школа, НШ-1044.2012.2, 2012-2013 гг.
- «Многоэлектронные эффекты в сверхпроводниках и магнетиках с синглетным основным состоянием», РФФИ № 13-02-01395, 2013-2015 гг.
- «Квантовые кластерные подходы в теории магнетизма», РФФИ № 14-02-31677, 2014-2015 гг.
- «Теория свойств решетки, электронных, магнитных и фононных возбуждений в сильно коррелированных материалах. Принципиальное развитие LDA+GTB и GW методов», РФФИ № 14-02-00186, 2014-2016 гг.
- «Теория электронной структуры сильно коррелированных систем, экспериментальное и теоретическое изучение электронных свойств и фазовых переходов в низкомерных системах с сильными электронными корреляциями», Грант президента РФ — ведущая научная школа, НШ-2886.2014.2, 2014-2015 гг.
- «Проведение научных исследований свойств сверхпроводящей и нормальной фаз сверхпроводников на основе железа и купратов под давлением», ФЦП «Научные и научно-педагогические кадры инновационной России» № 16.740.12.0731, 2011-2013 гг.
- «Проведение научных исследований в области методов диагностики перспективных наносистем с использованием источников синхротронного излучения», ФЦП «Научные и научно-педагогические кадры инновационной России» № 16.740.11.0740, 2011-2013 гг.
- «Магнетизм и сверхпроводимость в сильно коррелированных системах», Тематический план СФУ № 2.4491.2011, 2012-2013 гг.
- «Развитие кластерной теории возмущений в представлении Х-операторов Хаббарда для исследования систем с сильными электронными корреляциями», Грант Президента РФ для поддержки молодых российских ученых – кандидатов наук, МК-1168.2012.2, 2012-2013 гг.
- «Теоретические исследования пространственной и энергетической структуры конденсированного вещества», Госзадание Минобрнауки России №3085, 2014-2015 гг.
- «Развитие обобщенного метода сильной связи для расчета энергетической структуры магнитных систем с сильными кулоновскими корреляциями и сильным электрон-фононным взаимодействием», РНФ № 14-12-00061, 2014-2016 гг.
Премии, награды, конкурсы:
- Почётная грамота Министерства науки и высшего образования Российской Федерации, 2021 г.
- Премия банка МФК за вклад в развитие науки в области фундаментальной физики, 2014 г.
- Благодарственное письмо СФУ за активную работу по профессиональной ориентации учащихся, а также за активную жизненную позицию, 2013 г.
Увлечения, хобби:
- астрономия, походы


